Answer:
99.7% confidence interval is
![[0.4162,0.7437]](https://img.qammunity.org/2022/formulas/mathematics/college/o7sqz1ljhv50xt9f0bkzm65cz2llmypbt5.png)
Explanation:
The formula for a confidence interval for a population proportion is
 where
where
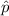 is the sample proportion,
is the sample proportion,
 is the sample size, and
is the sample size, and
 is the critical score for the desired confidence level.
is the critical score for the desired confidence level.
We are given a sample size of
 and a sample proportion of
and a sample proportion of
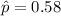 . Our critical score for a 99.7% confidence level would be
. Our critical score for a 99.7% confidence level would be
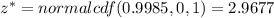
Therefore, the approximate 99.7% confidence interval for the population parameter is
![CI=\hat{p}\pm z^*\sqrt{\frac{\hat{p}(1-\hat{p})}{n} }=0.58\pm 2.9677\sqrt{(0.58(1-0.58))/(80) }=[0.4162,0.7438]](https://img.qammunity.org/2022/formulas/mathematics/college/138sb7x6hnevcni0rb1yfkzrveqq1ynrm1.png)
So we are 99.7% confident that the true population proportion is contained within the interval
![[0.4162,0.7437]](https://img.qammunity.org/2022/formulas/mathematics/college/o7sqz1ljhv50xt9f0bkzm65cz2llmypbt5.png)