Question

A soft drink machine outputs a mean of 2222 ounces per cup. The machine's output is normally distributed with a standard deviation of 44 ounces. What is the probability of filling a cup between 2525 and 3030 ounces? Round your answer to four decimal places.

Answer 1

Let X be the random variable for the output of the machine. Transform X to a standard normal random variable Z, using the rule

Z = (X - µ)/
`\sigma`

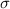
where µ and
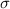`\sigma` are the mean and standard deviation of X.

Pr[25 < X < 30] = Pr[(25 - 22)/4 < (X - 22)/4 < (30 - 22)/4]

… = Pr[3/4 < Z < 2]

… = Pr[Z < 2] - Pr[Z < 3/4]

… ≈ 0.9773 - 0.7734

… ≈ 0.2039