Question

In the triangle EFG,

Answer 1

`4.\ \sin E = \cos G`

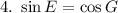
Explanation:

Given

`\triangle EFG`

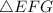
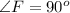`\angle F = 90^o` --- right angle

Required

Which of the options is true

In a triangle, we have:

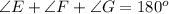`\angle E + \angle F + \angle G = 180^o` --- angles in a triangle

Substitute
`\angle F = 90^o`

`\angle E + 90^o + \angle G = 180^o`

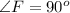
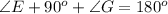
Collect like terms

`\angle E + \angle G = 180^o -90^o`

`\angle E + \angle G =90^o`

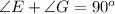
This implies that E and G are complementary angles.

For complementary angles, E and G;

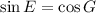`\sin E = \cos G` and
`\sin G = \cos E`

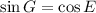
Hence, (4) is true