Answer:
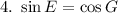
Explanation:
Given
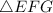
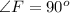 --- right angle
--- right angle
Required
Which of the options is true
In a triangle, we have:
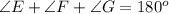 --- angles in a triangle
--- angles in a triangle
Substitute
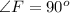
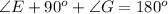
Collect like terms

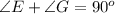
This implies that E and G are complementary angles.
For complementary angles, E and G;
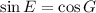 and
and
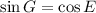
Hence, (4) is true