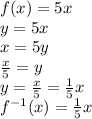Question

Can someone help!!!?

Answer 1

f^(-1)(x) = 1/5x

Explanation:

`\large{f(x) = mx + b \longrightarrow f^( - 1) (x) = (x - b)/(m) }`

Inverse Function is when we swap the x-term and y-term. Here is an explanation to the inverse of linear function above.

`\large{f(x) = mx + b}`

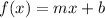
Here we define f(x) = y. It is better to use y instead of f(x)

`\large{y = mx + b}`

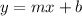
Swap x-term and y-term.

`\large{x = my + b}`

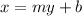
Arrange/Simplify in the y-isolated equation.

`\large{x - b = my} \\ \large {(x - b)/( m) = y} \\ \large{ y = (x - b)/(m) }`

Since the function is in inverse form. It's recommended to use f^(-1) to point out that the function is an inverse of the original function.

`\large \boxed{ {f}^( - 1) (x) = (x - b)/(m) }`

Hence, y = (x-b)/m is an inverse of y = mx+b. A one-to-one function can have an inverse form. Back to the question!

We are given the linear function:

`\large{f(x) = 5x}`

We will be using substitution method by substituting the original function in inverse form.

Since we know that the slope is 5 and doesn't have y-intercept which is b-value. Hence

`\large{ {f}^( - 1) (x) = (x - 0)/(5) } \\ \large{ {f}^( - 1) (x) = (x )/(5) } \\ \large{ {f}^( - 1) (x) = (1)/(5) x}`

Or we swap x-term and y-term.

`\large{f(x) = 5x} \\ \large{y = 5x} \\ \large{x = 5y} \\ \large{ (x)/(5) = y} \\ \large{y = (x)/(5) = (1)/(5) x} \\ \large{ {f}^( - 1) (x) = (1)/(5) x}`