A quadratic relation has zeros at 3 and –5. The parabola goes through the point (2, –14). What is the equation of the parabola in standard form?

Question

asked Feb 19, 2022 71.5k views

1 Answer

Gordonium · Answer 1 · 2022-02-26T04:31:59+0000

Answer:

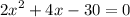
$\displaystyle 2 {x}^(2) + 4x - 30 = 0$

Explanation:

we are given the zeros and a point where it goes through of a quadratic equation

remember that when the roots are given then the function should be

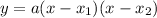
$\displaystyle \: y = a(x - x_(1))(x - x_(2))$

where a is the leading coefficient and x1 and x2 are the roots

substitute:

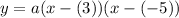
$\displaystyle y = a(x - (3))(x - ( - 5))$

simplify:

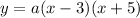
$\displaystyle y = a(x - 3)(x + 5)$

now the given point tells us that when x is 2 y is -14 therefore by using the point we can figure out a

substitute:

$\displaystyle a(2 - 3)(2 + 5) = - 14$

simplify parentheses:

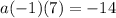
$\displaystyle a( - 1)(7) = - 14$

simplify multiplication:

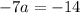
$\displaystyle - 7a = - 14$

divide both sides by -7:

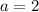
$\displaystyle a = 2$

altogether substitute:

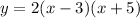
$\displaystyle y = 2(x - 3)(x + 5)$

since it want the equation y should be

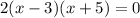
$\displaystyle 2(x - 3)(x + 5) = 0$

recall quadratic equation standard form:

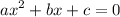
$\displaystyle {ax}^(2) + bx + c = 0$

so simplify parentheses:

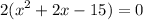
$\displaystyle 2( {x}^(2) + 2x - 15 ) = 0$

distribute:

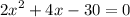
$\displaystyle 2 {x}^(2) + 4x - 30 = 0$

hence,

the equation of the parabola in standard form is 2x²+4x-30=0