Answer:
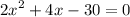
Explanation:
we are given the zeros and a point where it goes through of a quadratic equation
remember that when the roots are given then the function should be
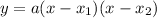
where a is the leading coefficient and x1 and x2 are the roots
substitute:
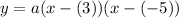
simplify:
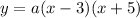
now the given point tells us that when x is 2 y is -14 therefore by using the point we can figure out a
substitute:
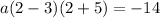
simplify parentheses:
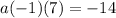
simplify multiplication:
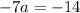
divide both sides by -7:
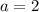
altogether substitute:
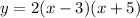
since it want the equation y should be
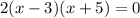
recall quadratic equation standard form:
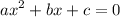
so simplify parentheses:
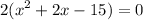
distribute:
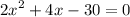
hence,
the equation of the parabola in standard form is 2x²+4x-30=0