Question

A 0.017 g coin sliding to the right at 0.255 m/s makes an elastic head-on collision with a 0.040 g coin that is initially at rest. After the collision, the 0.017 g coin moves to the left at 0.108 m/s. Find the final velocity of the other coin.

Answer 1

`\approx 0.154\:\mathrm{m/s}`

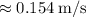
Step-by-step explanation:

In all collisions, whether elastic or inelastic, momentum must be conserved. Therefore, we can write an equation using the conservation of momentum:

`m_(c1)v_(c1,i)+m_(c2)v_(c2,i)=m_(c1)v_(c1,f)+m_(c2)v_(c2,f)`

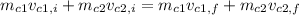
Solving for
`v_(2c,f)`:

`0.000017\cdot 0.255+0.000040\cdot0=0.000017\cdot (-0.108)+0.000040\cdot v_(c2,f),\\v_(c2,f)\approx \boxed{0.154\:\mathrm{m/s}}`

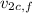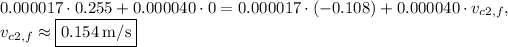
*Notes:

-It's important to convert g to kg, as kg is the SI unit of mass

-The negative sign in a velocity measure represents direction

-Since the velocity we solved for is positive, it implies that the direction is to the right