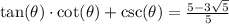Question

If cos() = − 2 3 and is in Quadrant III, find tan() cot() + csc(). Incorrect: Your answer is incorrect.

Answer 1

`\tan(\theta) \cdot \cot(\theta) + \csc(\theta) = (5 - 3\sqrt 5)/(5)`

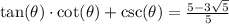
Explanation:

Given

`\cos(\theta) = -(2)/(3)`

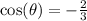
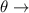`\theta \to` Quadrant III

Required

Determine
`\tan(\theta) \cdot \cot(\theta) + \csc(\theta)`

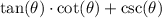
We have:

`\cos(\theta) = -(2)/(3)`

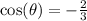
We know that:

`\sin^2(\theta) + \cos^2(\theta) = 1`

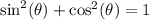
This gives:

`\sin^2(\theta) + (-(2)/(3))^2 = 1`

`\sin^2(\theta) + ((4)/(9)) = 1`

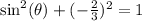
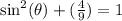
Collect like terms

`\sin^2(\theta) = 1 - (4)/(9)`

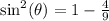
Take LCM and solve

`\sin^2(\theta) = (9 -4)/(9)`

`\sin^2(\theta) = (5)/(9)`

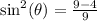
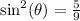
Take the square roots of both sides

`\sin(\theta) = \±(\sqrt 5)/(3)`

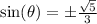
Sin is negative in quadrant III. So:

`\sin(\theta) = -(\sqrt 5)/(3)`

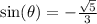
Calculate
`\csc(\theta)`

`\csc(\theta) = (1)/(\sin(\theta))`

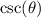
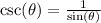
We have:
`\sin(\theta) = -(\sqrt 5)/(3)`

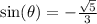
So:

`\csc(\theta) = (1)/(-(\sqrt 5)/(3))`

`\csc(\theta) = (-3)/(\sqrt 5)`

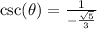
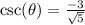
Rationalize

`\csc(\theta) = (-3)/(\sqrt 5)*(\sqrt 5)/(\sqrt 5)`

`\csc(\theta) = (-3\sqrt 5)/(5)`

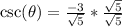
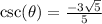
So, we have:

`\tan(\theta) \cdot \cot(\theta) + \csc(\theta)`

`\tan(\theta) \cdot \cot(\theta) + \csc(\theta) = \tan(\theta) \cdot (1)/(\tan(\theta)) + \csc(\theta)`

`\tan(\theta) \cdot \cot(\theta) + \csc(\theta) = 1 + \csc(\theta)`

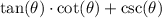
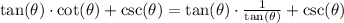
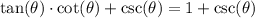
Substitute:
`\csc(\theta) = (-3\sqrt 5)/(5)`

`\tan(\theta) \cdot \cot(\theta) + \csc(\theta) = 1 -(3\sqrt 5)/(5)`

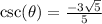
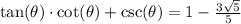
Take LCM

`\tan(\theta) \cdot \cot(\theta) + \csc(\theta) = (5 - 3\sqrt 5)/(5)`