Answer:
One solution
Explanation:
5x + y = 8
15x + 15y = 14
Lets solve using substitution, first we need to turn "5x + = 8" into "y = mx + b" or slope - intercept form
So we solve for "y" in the equation "5x + y = 8"
5x + y = 8
Step 1: Subtract 5x from both sides.
5x + y − 5x = 8 − 5x
Step 2: 5x subtracted by 5x cancel out and "8 - 5x" are flipped
y = −5x + 8
Now we can solve using substitution:
We substitute "-5x + 8" into the equation "15x + 15y = 14" for y
So it would look like this:
15x + 15(-5x + 8) = 14
Now we just solve for x
15x + (15)(−5x) + (15)(8) = 14(Distribute)
15x − 75x + 120 = 14
(15x − 75x) + (120) = 14(Combine Like Terms)
−60x + 120 = 14
Step 2: Subtract 120 from both sides.
−60x + 120 − 120 = 14 − 120
−60x = −106
Divide both sides by -60
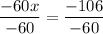
Simplify

Now that we know the value of x, we can solve for y in any of the equations, but let's use the equation "y = −5x + 8"
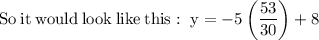
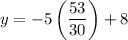
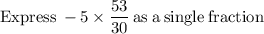
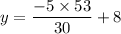
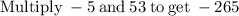
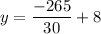
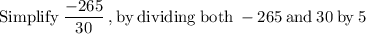
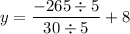


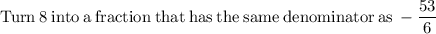
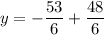


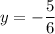

So there is only one solution to the equation.