Answer:
Fast ball challenge
Explanation:
Given
Slow Ball Challenge
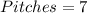


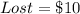
Fast Ball Challenge
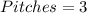
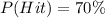

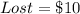
Required
Which should he choose?
To do this, we simply calculate the expected earnings of both.
Considering the slow ball challenge
First, we calculate the binomial probability that he hits all 7 pitches
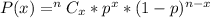
Where
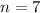 --- pitches
--- pitches
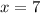 --- all hits
--- all hits
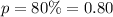 --- probability of hit
--- probability of hit
So, we have:
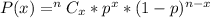
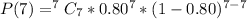
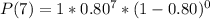
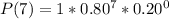
Using a calculator:
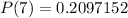 --- This is the probability that he wins
--- This is the probability that he wins
i.e.
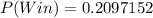
The probability that he lose is:
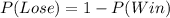 ---- Complement rule
---- Complement rule

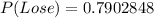
The expected value is then calculated as:
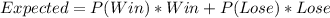
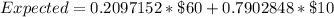
Using a calculator, we have:
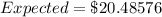
Considering the fast ball challenge
First, we calculate the binomial probability that he hits all 3 pitches
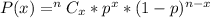
Where
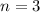 --- pitches
--- pitches
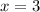 --- all hits
--- all hits
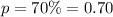 --- probability of hit
--- probability of hit
So, we have:
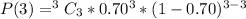
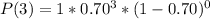
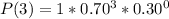
Using a calculator:
 --- This is the probability that he wins
--- This is the probability that he wins
i.e.
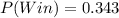
The probability that he lose is:
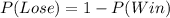 ---- Complement rule
---- Complement rule
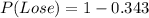
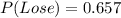
The expected value is then calculated as:
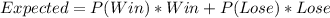
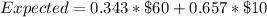
Using a calculator, we have:
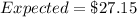
So, we have:
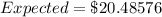 -- Slow ball
-- Slow ball
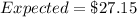 --- Fast ball
--- Fast ball
The expected earnings of the fast ball challenge is greater than that of the slow ball. Hence, he should choose the fast ball challenge.