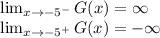Answer:
There is a vertical Asymptote at x = 5 because
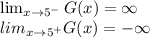
There is a vertical Asymptote at x = -5 because
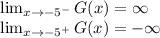
Explanation:
The exact question is as follows :
Given - G(x) = -7(x-5)^2(x+6)/(x-5)(x+5)
To find - Which statement make correctly uses limits determine a vertical Asymptote of G(x)
Solution -
Vertical Asymptotes are vertical lines which correspond to the zeroes of the denominator of a rational function.
Here the given function is the rational function
Denominator of G(x) = (x - 5)(x + 5)
So,
Put denominator = 0, we get
(x - 5)(x + 5) = 0
⇒x = 5, -5
∴ we get
G(x) has vertical Asymptotes at x = 5 and x = -5
Now,
At x= 5
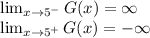
And
At x = -5
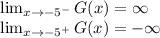
∴ we get
There is a vertical Asymptote at x = 5 because
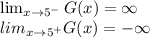
There is a vertical Asymptote at x = -5 because