Answer:
a) the ultimate tensile stress is 66717.8 psi
b) the ductility of the material in terms of percent elongation is 26%
Step-by-step explanation:
Given the data in the question;
ultimate load P = 13,100 lb
elongation δl = 0.52 in
diameter of specimen d = 0.50 in
gage length l = 2.00 inch
First we determine the cross-sectional area of the specimen
A =
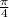 × d²
× d²
we substitute
A =
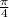 × ( 0.50 )²
× ( 0.50 )²
A = 0.1963495 in²
a) the ultimate tensile stress σ

tensile stress σ
 = P / A
= P / A
we substitute
tensile stress σ
 = 13,100 / 0.1963495
= 13,100 / 0.1963495
tensile stress σ
 = 66717.766 ≈ 66717.8 psi
= 66717.766 ≈ 66717.8 psi
Therefore, the ultimate tensile stress is 66717.8 psi
b) ductility of the material in terms of percent elongation;
percentage elongation of specimen = [change in length / original length]100
% = [ δl / l ]100
we substitute
% = [ 0.52 in / 2.00 in ]100
= [ 0.26 ]100
= 26
Therefore, the ductility of the material in terms of percent elongation is 26%