Answer:
a)
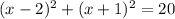
b)

Explanation:
a) the centre is (2,-1)
the equation so far is:
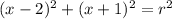
because you just change the sign of 2 to -2 and change the sign of -1 to +1
to find the radius:
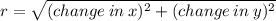

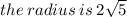
to find diameter square 2√5

b) find the gradient between the points (2,-1) and (4,-5)
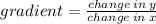

the gradient of the tangent is the negative reciprocal of -2. This means you flip it upside down which would be -1/2, then multiply by -1 which is 1/2
the gradient is 1/2
using the gradient and the point (4,-5) to write the equation in the form y=mx+c
here y is -5, m is the gradient (1/2) and x is 4
we need to work out c
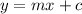

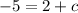
subtract 2 on both sides

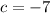
now the equation is
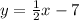
but we need to write it in the form ax+by+c=0
subtract y on both sides:
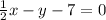
multiply everything by 2 to get rid of the fraction

that is the final equation