Question

Find the equation of a line which has 10 points the following two coordinates: (4, 0) and (3, 4)​

Answer 1

The equation of the line is y = -4·x + 16

10 points on the line include;

(0, 16), (1, 12), (2, 8), (3, 4), (4, 0), (5, -4), (6, -8), (7, 12), (8, -16), (9, -20), and (10, -24)

Step-by-step explanation:

The given points through which the line passes are;

(4, 0) and (3, 4)

The slope, 'm', of the line is given as follows;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

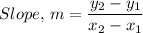
Therefore, the slope of the line is (4 - 0)/(3 - 4) = -4

In point and slope form we can get;

`(y-0)/(x-4) = -4`

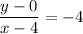
The equation of the line in point and slope form is therefore;

y = -4·(x - 4) = -4·x + 16

The equation of the line in slope and intercept form is

y = -4·x + 16

10 points on the line are obtained using the equation of the line and the desired x-values input into cells on MS Excel and presented here as follows;

(0, 16), (1, 12), (2, 8), (3, 4), (4, 0), (5, -4), (6, -8), (7, 12), (8, -16), (9, -20), and (10, -24)