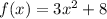Question

Solve the differential equation

Answer 1

`f(x) = 3x^2+8`

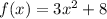
Explanation:

We are given the first derivative of
`f(x)` and the value of
`f(0)`.

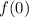To go from the first derivative to the original function, we integrate.

Therefore:

`f(x) = \int {6x} \, dx`

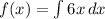
To integrate, we add 1 to the power and divide by the new power:

`\int {6x} \, dx = (6x^2)/(2) =3x^2+C`

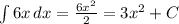
Because we have an indefinite integral, we have to add the constant,
`c`, to the end.

So:
`f(x) = 3x^2+C`

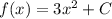
We know
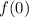`f(0)` so we can find the constant
`C`.

`f(0)=3(0)^2+C=8`

`C=8`

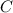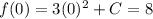
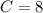
Therefore
`f(x) = 3x^2+8`