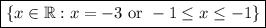Question

Solve the inequality |x+6-|3x+6||+|x+2|-x-4 less then or equal to 0

Answer 1

It looks like the inequality is

`\bigg|x + 6 - |3x + 6|\bigg| + |x + 2| - x - 4 \le 0`

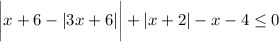
or equivalently,

`\bigg|x + 6 - 3 |x + 2|\bigg| + |x + 2| - x - 4 \le 0`

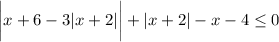
Recall the definition of absolute value:

`|x| = \begin{cases} x & \text{if } x \ge 0 \\ -x & \text{if } x < 0 \end{cases}`

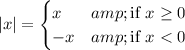
By this definition, we have

`|x + 2| = \begin{cases} x + 2 & \text{if } x + 2 \ge 0 \\ -(x + 2) & \text{if } x + 2 < 0 \end{cases} = \begin{cases} x + 2 & \text{if } x \ge -2 \\ -x - 2 & \text{if } x < -2 \end{cases}`

Suppose
`x < -2`. Then

`\bigg| x + 6 - |3x + 6| \bigg| + |x + 2| - x - 4 \\\\ = |x + 6 - 3 (-x - 2)| + (-x - 2) - x - 4 \\\\ = |4x + 12| - 2x - 6`

By definition of absolute value,

`|4x + 12| = 4 |x + 3| = \begin{cases} 4x + 12 & \text{if } x \ge -3 \\ -4x - 12 & \text{if } x < -3 \end{cases}`

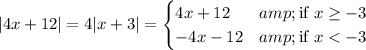
so we further suppose that
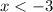`x < -3`. Then

`\bigg| x + 6 - |3x + 6| \bigg| + |x + 2| - x - 4 \\\\ = |4x + 12| - 2x - 6 \\\\ = (-4x - 12) - 2x - 6 \\\\ = -6x - 18 \le 0 \\\\ \implies x \ge -3`

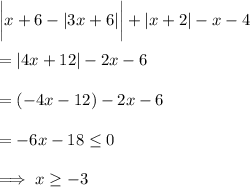
but this is a contradiction, so this case gives no solution.

If instead we have
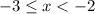`-3 \le x < -2`, then

`\bigg| x + 6 - |3x + 6| \bigg| + |x + 2| - x - 4 \\\\ = |4x + 12| - 2x - 6 \\\\ = (4x + 12) - 2x - 6 \\\\ = 2x + 6 \le 0 \\\\ \implies x \le -3`

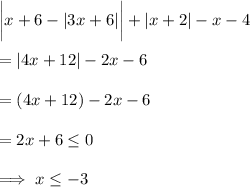
and
`-3 \le x` and
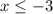`x \le -3` means that
`\boxed{x = -3}`.

Now suppose
`x \ge -2`. Then

`\bigg| x + 6 - |3x + 6| \bigg| + |x + 2| - x - 4 \\\\ = |x + 6 - 3 (x + 2)| + (x + 2) - x - 4 \\\\ = |-2x| - 2 \\\\ = 2 |x| - 2`

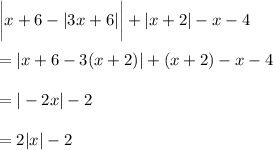
If we further suppose that
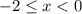`-2 \le x < 0`, then

`\bigg| x + 6 - |3x + 6| \bigg| + |x + 2| - x - 4 \\\\ = 2 |x| - 2 \\\\ = -2x - 2 \le 0 \\\\ \implies x \ge -1`

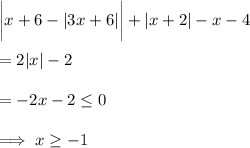
Otherwise, if
`x \ge 0`, then

`\bigg| x + 6 - |3x + 6| \bigg| + |x + 2| - x - 4 \\\\ = 2 |x| - 2 \\\\ = 2x - 2 \le 0 \\\\ \implies x \le 1`

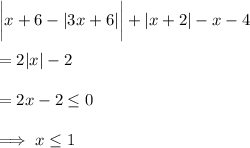
Taken together, this case gives the solution
`\boxed{-1 \le x \le 1}`

So, the overall solution to the inequality is the set

`\boxed{\left\{ x \in \mathbb R : x = -3 \text{ or } -1 \le x \le -1 \right\}}`