Question

Consider a set of cards that has four cards labeled 1, 2, 3, and 4. Suppose you pick two cards, without replacement, to obtain the mean of the two numbers that are drawn from the set. Which of the following tables shows the sampling distribution?

Answer 1

`\begin{array}{cccccc}{Mean} & {1.5} & {2} & {2.5} & {3} & {3.5}\ \\ {Probability} & {(1)/(6)} & {(1)/(6)} & {(1)/(3)} & {(1)/(6)} & {(1)/(6)}\ \end{array}`

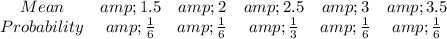
Step-by-step explanation:

Given

`Cards = \{1,2,3,4\}`

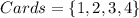
Required

The sampling distribution

The possible selection of 2 cards without replacement is as follows:

`S = \{(1,2) (1,3) (1,4) (2,1) (2,3) (2,4) (3,1) (3,2) (3,4) (4,1) (4,2) (4,3)\}`

Calculate the mean

List out the mean and the respective frequency

`1.5 \to 2`

`2 \to 2`

`2.5 \to 4`

`3 \to 2`

`3.5\to 2`

`Total \to 12`

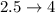
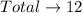
Calculate the probability of each mean

`P(1.5) \to (2)/(12) \to (1)/(6)\\`

`P(2) \to (2)/(12) \to (1)/(6)\\`

`P(2.5) \to (4)/(12) \to (1)/(3)\\`

`P(3) \to (2)/(12) \to (1)/(6)\\`

`P(3.5) \to (2)/(12) \to (1)/(6)`

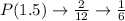
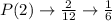
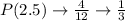
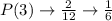
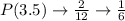
So, the table of sampling distribution is:

`\begin{array}{cccccc}{Mean} & {1.5} & {2} & {2.5} & {3} & {3.5}\ \\ {Probability} & {(1)/(6)} & {(1)/(6)} & {(1)/(3)} & {(1)/(6)} & {(1)/(6)}\ \end{array}`