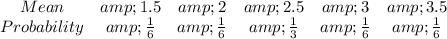Answer:
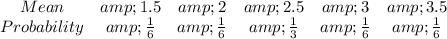
Step-by-step explanation:
Given
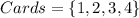
Required
The sampling distribution
The possible selection of 2 cards without replacement is as follows:
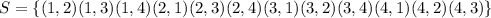
Calculate the mean
![\begin{array}{cccccccccccc}{Selection} & {(1,2)} & {(1,3)} & {(1,4)} & {(2,1)} & {(2,3)} & {(2,4)}& {(3,1)} & {(3,2)} & {(3,4)} & {(4,1)} & {(4,2)} & {(4,3)} \ \\ {Mean} & {1.5} & {2} & {2.5} & {1.5} & {2.5} & {3} & {2} & {2.5} & {3.5} & {2.5} & {3} & {3.5}\ \end{array}]()
List out the mean and the respective frequency


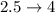


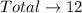
Calculate the probability of each mean
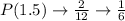
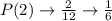
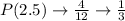
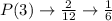
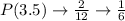
So, the table of sampling distribution is: