Question

Alejandra, the soccer player, runs 12 meters and kicks the ball into the air. It lands 20 meters away from her. 2

meters before the ball lands it is 2 meters in the air.

The flight of the ball is a parabola, what do we know about the parabola?

Answer 1

The focus of the parabola is (10, 10.0
`\overline 5`)

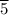The directrix of the parabola is, y = 1.0
`\overline 5`

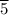
The maximum height reached by the ball = 5.
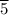`\overline 5` meters

The vertex of the parabola is (10, 5.
`\overline 5`)

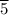Explanation:

The general equation of a parabola is y = a·(x - h)² + k

The vertex of the parabola = (h, k)

At 2 meters (horizontal) before landing, the height, h = 2 meters

∴ We have;

2 = a·(2 - h)² + k

2 = a·(18 - h)² + k

(2 - h)² = (18 - h)²

h² - 4·h + 4 = h² - 36·h + 324

36·h - 4·h = 324 - 4

h = 320/32 = 10

h = 10

2 = ut -0.5×9.81×t²

The

The time it takes the ball to fall 2 meters =

y = a·x² + b·x + c

h = -b/(2·a)

At y = 0, x = 0, therefore, c = 0

2 = a·2² + b·2 + c = 4·a + 2·b

2 = 324·a + 18·b

k = a·10² + b·10

20·a = -b

k = 100·a - 200·a = -100·a

2 = a·(2 - 10)² + k = 64·a + k

2 = 64·a + k = 64·a - 100·a = -36·a

a = 2/(-36) = -1/18

a = -1/18

a = 1/(4·p)

∴ 4·p = -18

p = 18/4 = 4.5

The focus of the parabola = (h, k + p) = (10, 10.0
`\overline 5`)

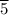The directrix, y = k - p = 1.0
`\overline 5`

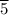
k = 100× -1/18 = 5.
`\overline 5`

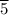
The maximum height reached by the ball = 5.
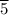`\overline 5` meters

The vertex of the parabola = (10, 5.
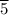`\overline 5`)