Answer:
The focus of the parabola is (10, 10.0
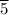 )
)
The directrix of the parabola is, y = 1.0
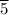
The maximum height reached by the ball = 5.
 meters
meters
The vertex of the parabola is (10, 5.
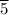 )
)
Explanation:
The general equation of a parabola is y = a·(x - h)² + k
The vertex of the parabola = (h, k)
At 2 meters (horizontal) before landing, the height, h = 2 meters
∴ We have;
2 = a·(2 - h)² + k
2 = a·(18 - h)² + k
(2 - h)² = (18 - h)²
h² - 4·h + 4 = h² - 36·h + 324
36·h - 4·h = 324 - 4
h = 320/32 = 10
h = 10
2 = ut -0.5×9.81×t²
The
The time it takes the ball to fall 2 meters =
y = a·x² + b·x + c
h = -b/(2·a)
At y = 0, x = 0, therefore, c = 0
2 = a·2² + b·2 + c = 4·a + 2·b
2 = 324·a + 18·b
k = a·10² + b·10
20·a = -b
k = 100·a - 200·a = -100·a
2 = a·(2 - 10)² + k = 64·a + k
2 = 64·a + k = 64·a - 100·a = -36·a
a = 2/(-36) = -1/18
a = -1/18
a = 1/(4·p)
∴ 4·p = -18
p = 18/4 = 4.5
The focus of the parabola = (h, k + p) = (10, 10.0
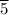 )
)
The directrix, y = k - p = 1.0
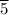
k = 100× -1/18 = 5.
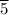
The maximum height reached by the ball = 5.
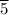 meters
meters
The vertex of the parabola = (10, 5.
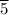 )
)