Answer:
66 ounces
Explanation:
To solve this, set up a fraction. Let "x" be the ounces of water after 5 seconds.
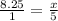
Step 1: Switch sides
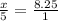
Step 2: Apply rule:
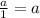
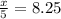
Step 3: Multiply both sides by 5
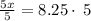
Step 4: Simplify
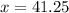
Now we have found the ounces of water in the container after 5 seconds, but already, there are 24.75 ounces before the ounces after 5 seconds. So to find the total add the given data to the found result
Step 1: Add 24.75 to 41.25
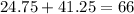
Therefore, there are 66 ounces after 5 seconds when 24.75 ounces are already in the container.