Question

Quadrilateral CDEF is inscribed in circle A. Which statements complete the proof to show that ∠CFE and ∠CDE are supplementary?

Quadrilateral CDEF is inscribed in circle A, so mARC CDE + mARC CFE= 360°. ∠CFE and ∠CDE are inscribed angles, which means that their measures are _________________. So, _________________. Using the substitution property of equality, 2 ⋅ m∠CFE + 2 ⋅ m∠CDE = 360°. Using the division property of equality, divide both sides of the equation by 2, resulting in m∠CFE + m∠CDE = 180°. Therefore, ∠CFE and ∠CDE are supplementary.

Answer 1

1/2 the measure of their intercepted arcs; m arc CDE= 2 ⋅ m∠CFE and arc CFE= 2 ⋅ m∠CDE (or C).

Explanation:

I just took the test and got this right :)

Answer 2

The statements that complete the proofs are;

First statement

One half the measure of their intercepted arcs

Second statement

mARC CDE = 2·m∠CFE and mARC CFE = 2·m∠CDE

Explanation:

The two column proof that ∠CFE and ∠CDE are supplementary is presented as follows;

Statement
`{}` Reason

Quadrilateral CDEF is inscribed is circle A
`{}` Given

`m\widehat{CDE}` +
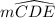`m\widehat{CFE}` = 360°
`{}` Measure of angle round a circle

∠CFE and ∠CDE are inscribed angles
`{}` Given

∠CFE + ∠CDE = 1/2 × (
`m\widehat{CDE}` +
`m\widehat{CFE}`)
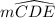`{}` Inscribed angles are (i) one half the measure of their intercepted arcs

2 × (∠CFE + ∠CDE) = (
`m\widehat{CDE}` +
`m\widehat{CFE}`)

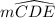So, (ii)
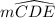`m\widehat{CDE}` = 2 × m∠CFE and
`m\widehat{CFE}` = 2 × m∠CDE From the inscribed angle theorem above (See attached drawing)

2·m∠CFE + 2·m∠CDE = 360°
`{}` Using substitution property of equality

(2·m∠CFE + 2·m∠CDE)/2 = 360°/2 → m∠CFE + m∠CDE) = 180°
`{}` Dividing both sides by 2

m∠CFE and m∠CDE) are supplementary
`{}` Angles that sum up to 180°

The statements that complete the proofs are;

(i) One half the measure of their intercepted arcs

(ii) mARC CDE = 2·m∠CFE and mARC CFE = 2·m∠CDE