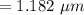Question

Coherent light with wavelength 591 nm passes through two very narrow slits, and the interference pattern is observed on a screen a distance of 3.00 m from the slits. The first-order bright fringe is a distance of 4.84 mm from the center of the central bright fringe. For what wavelength of light will the first-order dark fringe be observed at this same point on the screen?

Answer 1

The wavelength will be "1.182 μm".

Step-by-step explanation:

The given values are:

Wavelength

`\lambda=591 \ nm`

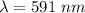
or,

`=591* 10^-9 \ m`

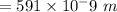
Distance,

`d = 3.00 m`

`n = 1`

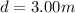
Distance of fringe from center,

`y = 4.84 \ mm`

We have to find the wavelength of first order dark fringe,

`\lambda = ?`

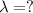
As we know,

⇒
`y_(bright) =(1* \lambda* L)/(d)`

On putting the given values in the formula, we get

`0.00484=(1* (591* 10^(-9))* 3)/(d)`

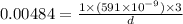
On applying the cross multiplication, we get

`\lambda = (0.00484* 000036632)/(0.5* 3)`

`=1182* 10^(-9)`

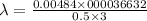
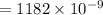
or,

`=1.182 \ \mu m`