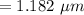Answer:
The wavelength will be "1.182 μm".
Step-by-step explanation:
The given values are:
Wavelength
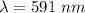
or,
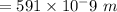
Distance,
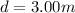
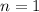
Distance of fringe from center,
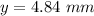
We have to find the wavelength of first order dark fringe,
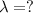
As we know,
⇒
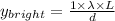
On putting the given values in the formula, we get
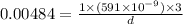
On applying the cross multiplication, we get
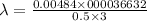
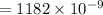
or,