Question

Consider a father pushing a child on a playground merry-go-round. The system has a moment of inertia of 84.4 kg.m^2. The father exerts a force on the merry-go-round perpendicular to its radius to achieve an angular acceleration of 4.44 rad/s^2.

Required:
a. How long (in s) does it take the father to give the merry-go-round an angular velocity of 1.53 rad/s? (Assume the merry-go-round is initially at rest.)
b. How many revolutions must he go through to generate this velocity?
c. If he exerts a slowing force of 270 N at a radius of 1.20 m, how long (in s) would it take him to stop them?

Answer 1

Step-by-step explanation:

Given that:

the initial angular velocity
`\omega_o = 0`

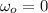
angular acceleration
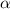`\alpha` = 4.44 rad/s²

Using the formula:

`\omega = \omega_o+ \alpha t`

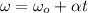
Making t the subject of the formula:

`t= (\omega- \omega_o)/( \alpha )`

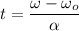
where;

`\omega = 1.53 \ rad/s^2`

∴

`t= (1.53-0)/(4.44 )`

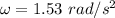
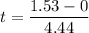
t = 0.345 s

b)

Using the formula:

`\omega ^2 = \omega _o^2 + 2 \alpha \theta`

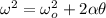
here;

`\theta` = angular displacement

∴

`\theta = (\omega^2 - \omega_o^2)/(2 \alpha )`

`\theta = ((1.53)^2 -0^2)/(2 (4.44) )`

`\theta =0.264 \ rad`

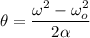
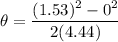
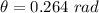
Recall that:

2π rad = 1 revolution

Then;

0.264 rad = (x) revolution

`x = (0.264 * 1)/(2 \pi)`

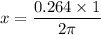
x = 0.042 revolutions

c)

Here; force = 270 N

radius = 1.20 m

The torque = F * r

`\tau = 270 * 1.20 \\ \\ \tau = 324 \ Nm`

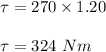
However;

From the moment of inertia;

`Torque( \tau) = I \alpha \\ \\ Since( I \alpha) = 324 \ Nm. \\ \\ Then; \\ \\ \alpha= (324)/(I)`

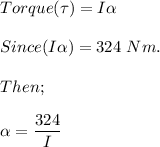
given that;

I = 84.4 kg.m²

`\alpha= (324)/(84.4) \\ \\ \alpha=3.84 \ rad/s^2`

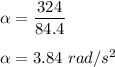
For re-tardation;
`\alpha=-3.84 \ rad/s^2`

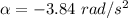
Using the equation

`t= (\omega- \omega_o)/( \alpha )`

`t= (0-1.53)/( -3.84 )`

`t= (1.53)/( 3.84 )`

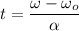
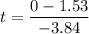
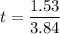
t = 0.398s

The required time it takes= 0.398s