Answer:
Step-by-step explanation:
Given that:
the initial angular velocity
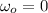
angular acceleration
 = 4.44 rad/s²
= 4.44 rad/s²
Using the formula:
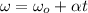
Making t the subject of the formula:
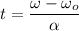
where;
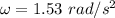
∴
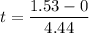
t = 0.345 s
b)
Using the formula:
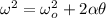
here;
 = angular displacement
= angular displacement
∴
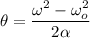
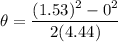
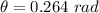
Recall that:
2π rad = 1 revolution
Then;
0.264 rad = (x) revolution

x = 0.042 revolutions
c)
Here; force = 270 N
radius = 1.20 m
The torque = F * r
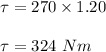
However;
From the moment of inertia;
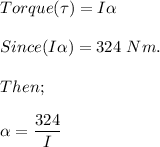
given that;
I = 84.4 kg.m²
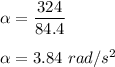
For re-tardation;
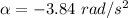
Using the equation
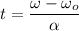
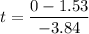
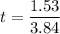
t = 0.398s
The required time it takes= 0.398s