Question

A steel wire is suspended vertically from its upper end. The wire is 400 ft long and has a diameter of 3/16 in. The unit weight of steel is 490 pcf. Compute:

a. the maximum tensile stress due to the weight of the wire
b. the maximum load P that could be supported at the lower end of the wire. Allowable tensile stress is 24,000 psi.

Answer 1

a) the maximum tensile stress due to the weight of the wire is 1361.23 psi

b) the maximum load P that could be supported at the lower end of the wire is 624.83 lb

Step-by-step explanation:

Given the data in the question;

Length of wire L = 400 ft = ( 400 × 12 )in = 4800 in

Diameter d = 3/16 in

Unit weight w = 490 pcf

First we determine the area of the wire;

A = π/4 × d²

we substitute

A = π/4 × (3/16)²

A = 0.0276 in²

Next we get the Volume

V = Area × Length of wire

we substitute

V = 0.0276 × 4800

V = 132.48 in³

Weight of the steel wire will be;

W = Unit weight × Volume

we substitute

W = 490 × ( 132.48 / 12³ )

W = 490 × 0.076666

W = 37.57 lb

a) the maximum tensile stress due to the weight of the wire;

σ
`_w` = W / A

we substitute

σ
`_w` = 37.57 / 0.0276

= 1361.23 psi

Therefore, the maximum tensile stress due to the weight of the wire is 1361.23 psi

b) the maximum load P that could be supported at the lower end of the wire. Allowable tensile stress is 24,000 psi

Maximum load P that the wire can safely support its lower end will be;

P = ( σ
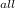`_{all` - σ
`_w` )A

we substitute

P = ( 24000 - 1361.23 )0.0276

P = 22638.77 × 0.0276

P = 624.83 lb

Therefore, the maximum load P that could be supported at the lower end of the wire is 624.83 lb