Answer:
a. The margin of error for the survey is of 0.0308 = 3.08%.
b. The 95% confidence interval that is likely to contain the exact percent of all people who favor the home team winning is (65.96%, 78.04%).
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the z-score that has a p-value of
 .
.
The margin of error of the survey is:
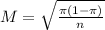
The confidence interval can be written as:
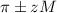
In a survey of 212 people at the local track and field championship, 72% favored the home team winning.
This means that
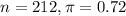
a. Find the margin of error for the survey.

The margin of error for the survey is of 0.0308 = 3.08%.
b. Give the 95% confidence interval that is likely to contain the exact percent of all people who favor the home team winning.
95% confidence level
So
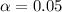 , z is the value of Z that has a p-value of
, z is the value of Z that has a p-value of
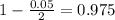 , so
, so
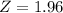 .
.
Lower bound:

Upper bound:
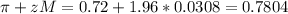
As percent:
0.6596*100% = 65.96%
0.7804*100% = 78.04%.
The 95% confidence interval that is likely to contain the exact percent of all people who favor the home team winning is (65.96%, 78.04%).