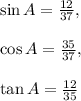Question

Need cos A and tan A asap please

Answer 1

Explanation:

sin A=opposite/hypotenuse=12/37

cos A=adjacent/hypotenuse=35/37

tan A=opposite/adjacent=12/35

Answer 2

`\sin A=(12)/(37),\\\\\cos A=(35)/(37),\\\\\tan A=(12)/(35)`

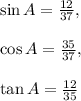
Explanation:

In a right triangle only, the sine of an angle is equal to the angle's opposite side divided by the hypotenuse of the triangle. (o/h)

The cosine of the angle is equal to the angle's adjacent side divided by the hypotenuse of the triangle. (a/h)

The tangent of the angle is equal to angle's opposite side divided by the adjacent side. (o/a)

In this case, angle A's opposite side is 12, its adjacent side is 35, and the hypotenuse is 37 (o=12, a=35, h=37).

Thus we have:

`\sin A=(12)/(37),\\\\\cos A=(35)/(37),\\\\\tan A=(12)/(35)`