Answer:
a. E = 2452.5 J = 2.45 KJ
b. P.E = 981 J = 0.98 KJ
c. K.E = 1471.5 J = 1.47 KJ
d. vf = 14 m/s
Step-by-step explanation:
a.
At the highest point the total energy is equal to the potential energy of the object:
E = Potential Energy = mgh
where,
E = Total energy =?
m = mass of object = 25 kg
g = acceleration due to gravity = 9.81 m/s²
h = height = 10 m
Theerfore,
E = (25 kg)(9.81 m/s²)(10 m)
E = 2452.5 J = 2.45 KJ
b.
P.E = mgh
where,
h = 4 m
Therefore,
P.E = (25 kg)(9.81 m/s²)(4 m)
P.E = 981 J = 0.98 KJ
c.
First, we will find the velocity at 4 m by using the third equation of motion:
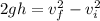
where,
h = height lost = 10 m - 4 m = 6 m
vf = final speed = ?
vi = initial speed = 0 m/s
Therefore,
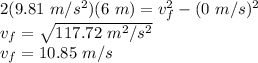
Hence, the kinetic energy will be:
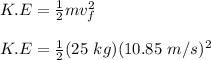
K.E = 1471.5 J = 1.47 KJ
d.
We will find the velocity at the bottom by using the third equation of motion:
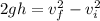
where,
h = height lost = 10 m
vf = final speed = ?
vi = initial speed = 0 m/s
Therefore,
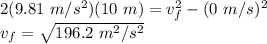
vf = 14 m/s