Question

An object of mass 25kg is falling from the height h=10 m. calculate

a. The total energy of an object at h=10m.
b. Potential energy of the object when it is at h= 4m
c. Kinetic energy of the object when it is at h= 4m
d. What will be the speed of the object when it hits the ground?​

Answer 1

a. E = 2452.5 J = 2.45 KJ

b. P.E = 981 J = 0.98 KJ

c. K.E = 1471.5 J = 1.47 KJ

d. vf = 14 m/s

Step-by-step explanation:

a.

At the highest point the total energy is equal to the potential energy of the object:

E = Potential Energy = mgh

where,

E = Total energy =?

m = mass of object = 25 kg

g = acceleration due to gravity = 9.81 m/s²

h = height = 10 m

Theerfore,

E = (25 kg)(9.81 m/s²)(10 m)

E = 2452.5 J = 2.45 KJ

b.

P.E = mgh

where,

h = 4 m

Therefore,

P.E = (25 kg)(9.81 m/s²)(4 m)

P.E = 981 J = 0.98 KJ

c.

First, we will find the velocity at 4 m by using the third equation of motion:

`2gh = v_f^2-v_i^2`

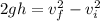
where,

h = height lost = 10 m - 4 m = 6 m

vf = final speed = ?

vi = initial speed = 0 m/s

Therefore,

`2(9.81\ m/s^2)(6\ m) = v_f^2-(0\ m/s)^2\\v_f = √(117.72\ m^2/s^2) \\v_f = 10.85\ m/s`

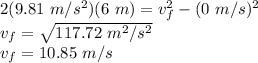
Hence, the kinetic energy will be:

`K.E = (1)/(2) mv_f^2\\\\K.E = (1)/(2) (25\ kg)(10.85\ m/s)^2`

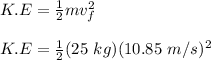
K.E = 1471.5 J = 1.47 KJ

d.

We will find the velocity at the bottom by using the third equation of motion:

`2gh = v_f^2-v_i^2`

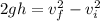
where,

h = height lost = 10 m

vf = final speed = ?

vi = initial speed = 0 m/s

Therefore,

`2(9.81\ m/s^2)(10\ m) = v_f^2-(0\ m/s)^2\\v_f = √(196.2\ m^2/s^2) \\`

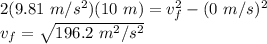
vf = 14 m/s