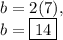Question

The area of a right triangle is 49 square inches. The base is

twice as long as the height. The formula for the area of a
triangle is A = 1/2 bh, where b is the base and h is the height.
How long is the base and how tall is the height?

Answer 1

`h=7,\\b=14`

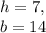
Explanation:

Since the base is twice as long as the height, set up the following proportion:

`b=2h`.

The area of the a right triangle is equal to
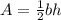`A=(1)/(2)bh`, where
`b` is a base of the triangle and
`h` is the respective height.

To solve for height, set up the equation (substituing
`b=2h`:

`(1)/(2)\cdot2h\cdot h=49,\\2h^2=98,\\h^2=49,\\h=\boxed{7}`

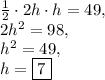
To solve for base, substitute
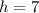`h=7` in the proportion
`b=2h`:

`b=2(7),\\b=\boxed{14}`

Answer 2

height: 7 in

base: 14 in

Explanation:

Let the height of the triangle equal x. This means that the base can be represented by the expression 2x. Now we plug these values into the area formula for a triangle:

A = bh / 2

49 = x * 2x / 2

And simplify

49 = x^2

We can find the square root of both sides to get x = 7, so the height is 7 inches. Since the base is twice the height, it is 14 inches.