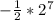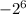Question

Find the 8th term in the

sequence
-1/2,-1, -2, -4,...
Hint: Write a formula to help you.
1st term . Common Ratio desired term – 1)

Answer 1

-64

Explanation:

By looking at the numbers, we can identify that this is a geometric sequence and the ratio would be 2. The formula to find the nth term in a geometric series is:

`t *r^(n-1)`

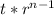
where t is the first term and r is the ratio. We can substitute in the information we know:

`-(1)/(2) *2^(n-1)`

We are looking for the eighth term, so we substitute 8 where n is:

`-(1)/(2)*2^(8-1)`

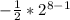
We can simplify:

`-(1)/(2)*2^7`

`-2^6`

`-64`