Answer:
Option 3
Explanation:
If two ratios
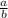 and
and
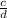 are proportional,
are proportional,
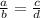
By applying this property for the given options,
Option 1
If the given ratios
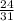 and
and
 are proportional.
are proportional.
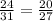
Which is false.
Therefore, ratios are not proportional.
Option 2
If the given ratios
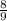 and
and
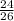 are proportional,
are proportional,
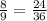
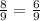
False.
Therefore, given ratios are not proportional.
Option 3
If the given ratios
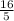 and
and
 are proportional,
are proportional,
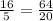
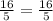
True.
Therefore, the given ratios are proportional.
Option 4
If the given ratios
 and
and
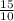 are proportional,
are proportional,
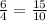

True.
Therefore, given ratios are proportional.
Option 3 is the answer.