Question

Marjorie drops an object from a height of h meters, and it hits the ground with a velocity of v m/s, as given by the function v equals square root of 19.6 h. If the velocity of the object is 81.4 m/s, what was the height of the object before it was dropped? Round your answer to the nearest tenth.

Answer 1

To find the height from which Marjorie dropped the object, square the velocity and divide by 19.6. With a velocity of 81.4 m/s, the height is approximately 337.4 meters.

Step-by-step explanation:

The student's question is about determining the height an object was dropped from, based on its final velocity just before hitting the ground. The equation provided, v = √(19.6h), where v is the final velocity and h is the height, can be used to solve for the height. Given that the final velocity v is 81.4 m/s, we can rearrange the equation to solve for h: h = v2 / 19.6. Plugging in the values, h = 81.42 / 19.6 which equals approximately 337.4 meters. This would be rounded to 337.4 meters to the nearest tenth.

Answer 2

The object was dropped at a height of 338.1 meters.

Step-by-step explanation:

According to the statement, the function velocity (
`v`), in meters per second, in term of the initial height of the object (
`h`), in meters, is represented by:

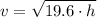`v = √(19.6\cdot h)` (1)

This formula represents a particular case of a free fall analyzed by means of the Principle of Energy Conservation. If we know that
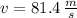`v = 81.4\,(m)/(s)`, then the height of the object before being dropped is:

`h = (v^(2))/(19.6)`

`h = 338.059\,m`

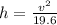
The object was dropped at a height of 338.1 meters.