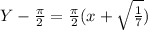Question

Find the tangent line equation of the curve at the given point. Y=arcsin(7x) at the point where x=sqrt2/14

Answer 1

`Y-(\pi)/(2) =(\pi)/(2) (x+\sqrt{(1)/(7)})`

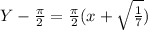
Explanation:

The equation of the curve is

`Y = sin^(-1)(7x)`

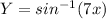
To find the equation of tangent we need to differentiate this equation w.r.t x

So, differentiating we get

`Y'=(7)/(√(1-49x^2) )`

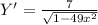
This would give the slope of the tangent line at any given point of which x coordinate is known. In the present case it is
`x = \sqrt{(1)/(7) }`

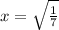
Then slope would accordingly be

`Y'=(7)/(√(1-49/49) )`

= ∞

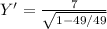
For,
`x = \sqrt{(1)/(7) }`,
`Y = sin^(-1)(7/7)= \pi/2`

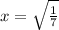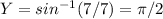
Equation of tangent line, in the point slope form, would be
`Y-(\pi)/(2) =(\pi)/(2) (x+\sqrt{(1)/(7)})`