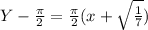Answer:
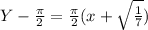
Explanation:
The equation of the curve is
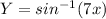
To find the equation of tangent we need to differentiate this equation w.r.t x
So, differentiating we get
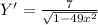
This would give the slope of the tangent line at any given point of which x coordinate is known. In the present case it is
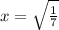
Then slope would accordingly be
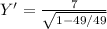
= ∞
For,
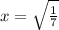 ,
,
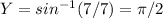
Equation of tangent line, in the point slope form, would be