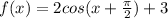Question

17. Identify the amplitude, period, and vertical shift for the

function shown. Then write an equation that represents the curve.
m
A=
B=
P=
C=
f(x)=

Answer 1

`f(x)=2cos(x+(\pi)/(2))+3`

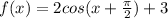
Explanation:

Because the function is symmetric about the y-axis, using the cosine function is most appropriate.

Refer to the equation for a cosine function:

`f(x)=acos(bx+c)+d`

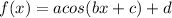
Amplitude:
`|a|`

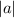
Period:
`(2\pi)/(|b|)`

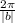
Phase shift:
`-(c)/(b)`

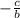
Midline:
`y=d`

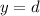
The amplitude would be the average of the maximum and minimum y-values of the function, which would be
`|a|=|(5-1)/(2)| =|(4)/(2)| =|2|=2`.

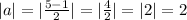The value of
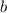`b` in
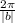`(2\pi)/(|b|)` represents the length of the period, so since the length of the period is
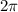`2\pi`, this means that
`b=(2\pi)/(|2\pi|) =1`.

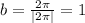The phase shift,
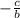`-(c)/(b)`, describes the horizontal shift of a function. Because the phase shift is
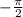`-(\pi)/(2)`, then we can set up the equation
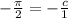`-(\pi)/(2)=-(c)/(1)` where we determine
`c=(\pi)/(2)`.

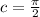The midline (or vertical shift),
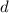`d`, is the horizontal line that passes through between the maximum and minimum points, which the function oscillates. In this case, the midline would be located at the line
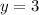`y=3`, therefore,
`d=3`.

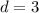Putting all our information together, your final equation is:

`f(x)=2cos(x+(\pi)/(2))+3`