Answer:

Explanation:
Because the function is symmetric about the y-axis, using the cosine function is most appropriate.
Refer to the equation for a cosine function:
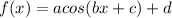
Amplitude:
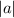
Period:
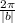
Phase shift:
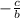
Midline:
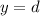
The amplitude would be the average of the maximum and minimum y-values of the function, which would be
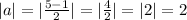 .
.
The value of
 in
in
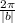 represents the length of the period, so since the length of the period is
represents the length of the period, so since the length of the period is
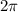 , this means that
, this means that
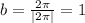 .
.
The phase shift,
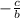 , describes the horizontal shift of a function. Because the phase shift is
, describes the horizontal shift of a function. Because the phase shift is
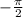 , then we can set up the equation
, then we can set up the equation
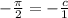 where we determine
where we determine
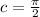 .
.
The midline (or vertical shift),
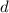 , is the horizontal line that passes through between the maximum and minimum points, which the function oscillates. In this case, the midline would be located at the line
, is the horizontal line that passes through between the maximum and minimum points, which the function oscillates. In this case, the midline would be located at the line
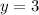 , therefore,
, therefore,
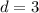 .
.
Putting all our information together, your final equation is:
