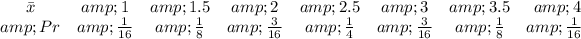Question

Consider the set {1, 2, 3, 4}.

a. Make a list of all samples of size 2 that can be drawn from this set of integers.
b. Construct the sampling distribution of sample means for samples of size 2 selected from this set.
c. Provide the distribution both in the form of a table and histogram.

Answer 1

(a)

`List = \{(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),\\(4,1),(4,2),(4,3).(4,4)\}`

(b) Sampling Distribution (Table)

`\begin{array}{cccccccc}{\bar x} & {1} & {1.5} & {2} & {2.5} & {3} & {3.5} & {4} & {Pr}& {(1)/(16)} & {(1)/(8)} & {(3)/(16)} & {(1)/(4)} & {(3)/(16)} & {(1)/(8)} & {(1)/(16)} \ \end{array}`

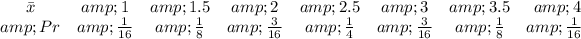
(b) Sampling Distribution (Histogram)

See attachment

Explanation:

Given

`Set = \{1,2,3,4\}`

`n =4`

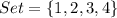
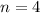
Solving (a): A list of sample size 2

We have:

`n =4`

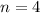
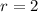`r = 2` --- the sample size

First, we calculate the number of list using permutation (orders matter)

`n(List) = n^r`

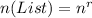
So, we have:

`n(List) = 4^2`

`n(List) = 16`

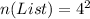
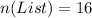
And the list is:

`List = \{(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),\\(4,1),(4,2),(4,3).(4,4)\}`

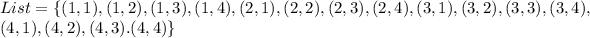
Solving (b): Sample distribution of sample means of (a)

First, calculate the mean of each set using:

`Mean = (Sum)/(2)`

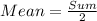
So, we have:

`(1,1) \to (1+1)/(2) \to 1`
`(1,2) \to (1+2)/(2) \to 1.5`
`(1,3) \to (1+3)/(2) \to 2`
`(1,4) \to (1+4)/(2) \to 2.5`

`(2,1) \to (2+1)/(2) \to 1.5`
`(2,2) \to (2+2)/(2) \to 2`
`(2,3) \to (2+3)/(2) \to 2.5`
`(2,4) \to (2+4)/(2) \to 3`

`(3,1) \to (3+1)/(2) \to 2`
`(3,2) \to (3+2)/(2) \to 2.5`
`(3,3) \to (3+3)/(2) \to 3`
`(3,4) \to (3+4)/(2) \to 3.5`

`(4,1) \to (4+1)/(2) \to 2.5`
`(4,2) \to (4+2)/(2) \to 3`
`(4,3) \to (4+3)/(2) \to 3.5`
`(4,4) \to (4+4)/(2) \to 4`

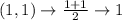
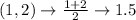
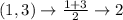
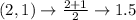
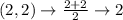
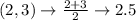
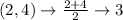
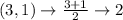
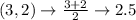
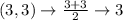
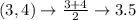
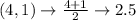
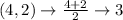
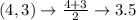
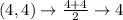
Write out the sample means (sorted)

`\bar x =\{1,1.5,1.5,2,2,2,2.5,2.5,2.5,2.5,3,3,3,3.5,3.5,4\}`

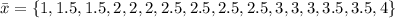
Construct a frequency table

`\begin{array}{cc}{\bar x} & {f} & {1} & {1} & {1.5} & {2} & {2} & {3} & {2.5} & {4} & {3} & {3} & {3.5} &{2} & {4} & {1} & Total & 16\ \end{array}`

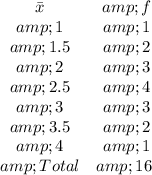
Construct the sampling distribution where the probability is calculated using:
`(f)/(Total)`

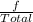
So, we have:

`\begin{array}{cccccccc}{\bar x} & {1} & {1.5} & {2} & {2.5} & {3} & {3.5} & {4} & {Pr}& {(1)/(16)} & {(1)/(8)} & {(3)/(16)} & {(1)/(4)} & {(3)/(16)} & {(1)/(8)} & {(1)/(16)} \ \end{array}`