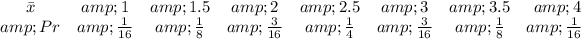Answer:
(a)
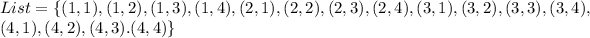
(b) Sampling Distribution (Table)
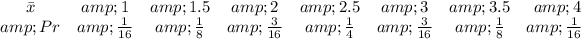
(b) Sampling Distribution (Histogram)
See attachment
Explanation:
Given
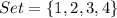
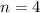
Solving (a): A list of sample size 2
We have:
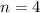
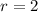 --- the sample size
--- the sample size
First, we calculate the number of list using permutation (orders matter)
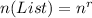
So, we have:
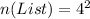
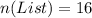
And the list is:
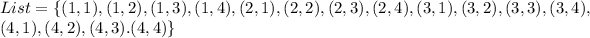
Solving (b): Sample distribution of sample means of (a)
First, calculate the mean of each set using:

So, we have:
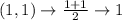
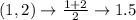
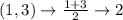
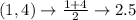
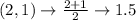
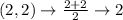
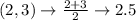
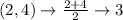

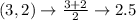
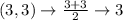
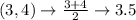
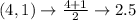
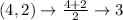
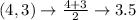
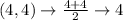
Write out the sample means (sorted)
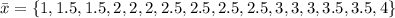
Construct a frequency table
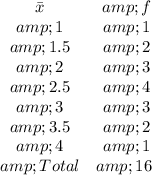
Construct the sampling distribution where the probability is calculated using:
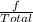
So, we have: