Question

An initially uncharged sphere is on an insulated stand and isolated in a chamber. The charge on the sphere is monitored as a beam of monochromatic light shines on the sphere. Initially nothing happens. The wavelength of the light is slowly decreased. When the wavelength reaches a certain value, a positive charge is suddenly measured on the sphere. The wavelength is then held constant, and the charge continues to increase at a constant rate. The intensity of the beam is then increased without the wavelength being changed, and the rate of increase of the charge becomes greater.

Required:
a. In a coherent paragraph-length response, describe the cause of the charge on the sphere and the changes in the observations about the charge, in terms of physics principles.
b. An electron in the chamber is moving with speed 2×10^5m/s when it collides with a positron (a particle identical to an electron except for the sign of its charge) moving with the same speed in the opposite direction. The particles annihilate each other. How much energy is released due to the annihilation?
c. In another experiment, a beam of electrons with uniform wavelength λe is incident on a slit, where the width of the slit is much larger than λe. A detector is placed near the slit, but no diffraction pattern is observed. What change should be made that would result in a diffraction pattern? Indicate why this change is the one needed.

Answer 1

a) E = K + Φ, b) ΔE = 1.64 10⁻¹³ J., c) λ = a

Step-by-step explanation:

a) In this case it is an example of the photoelectric effect that was correctly described by Einstein assuming that the light ray is composed of a series of particles called photons, each one with an energy given by the Planck equation

E = h f

c = λ f

substituting

E = h c /λ

We can see from this equation that as the wavelength of the ray decreases the energy of each photon increases, the moment arrives that the energy is sufficient to remove an electron from the sphere, thus leaving an unbalanced positive charge, this description explains why the positive charge appears on the sphere; the minimum wavelength to remove an electron is

E = K + Φ

if K = 0

E =Φ

where fi is the work function of the material.

When the intensity of the ray increases according to Eintein's description, the number of photons increases, so if the number of photons increases, the number of shocks and the number of electrons expelled increases, therefore the unbalanced positive charge also increases.

b) the energy released in collision is the sum of the energy of each particle

for the electron

E = K + m c² = (pc) ² + (m c²) ²

where the moment is

p = γ m u

γ =
`\sqrt{1- ((u)/(c))^2 }`

γ =
`\sqrt {1- ( (2 \ 10^5)/(3 \ 10^8 ))^2 } = \sqrt{1- (6.67 \ 10 ^(-4)^2 )`

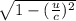
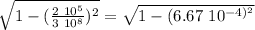
γ ≅ 1

in this case since the speed of the particles is much less than the speed of light,

E = (m u) ² + (m c²) ²

E = m² (u² + c²)

E = 9.1 10⁻³¹ [(2 10⁵) ² + (3 10⁸) ²

E = 9.1 10⁻³¹ 9 10¹⁶

E = 8.2 10⁻¹⁴ J

the positron has an energy of equal magnitude, so when the two particles annihilate the energy change is

ΔE = 2E

ΔE = 2 (8.2 10⁻¹⁴)

ΔE = 1.64 10⁻¹³ J.

c) the expression that describes the diffraction process is

a sin θ = m λ

sin θ = m λ/ a

where a is the width of the slit and m in diffraction order

The greatest value that the sine function can have is 1

1 = m λ / a

λ = a / m

therefore we can see that to see the diffraction phenomenon the width of the slit must be greater than or equal to the wavelength