Answer:
The volume of can A is half the volume of can B.
Explanation:
Given
Can A and Can B
Required
The true statement
For Can A, we have:
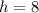
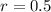
The volume is:
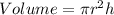
This gives:
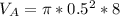
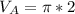
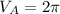
For Can B, we have:
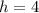
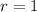
The volume is:
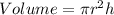
This gives:
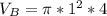
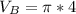
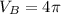
So, we have:
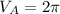
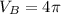
By comparison, (d) is correct