1 Answer

Dscyre Scotti · Answer 1 · 2023-05-01T01:08:07+0000

Answer:

(63)/(65)

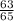
Explanation:

The angle theta terminates in quadrant 4, so we know
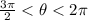$(3\pi)/(2) < \theta < 2\pi$ and that the sin is negative and the cos is positive.

Using the Pythagorean identity
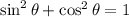$\sin^2\theta+\cos^2\theta=1$ , we substitute
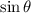$\sin\theta$ to find
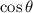$\cos\theta$ :

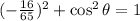$(-(16)/(65))^2+\cos^2\theta=1$ .

Solving for
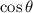$\cos\theta$ , we have

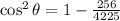$\cos^2\theta=1-(256)/(4225)\\$ ,

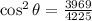$\cos^2\theta=(3969)/(4225)$ .

Taking the square root of both sides gives

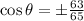$\cos\theta=\pm(63)/(65)$ .

We found before that since the angle theta terminates in quadrant 4, the cos is positive, so we take the positive square root to get

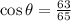$\cos\theta=(63)/(65)$ .

Please log in or register to add a comment.