Answer:

Explanation:
The angle theta terminates in quadrant 4, so we know
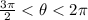 and that the sin is negative and the cos is positive.
and that the sin is negative and the cos is positive.
Using the Pythagorean identity
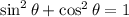 , we substitute
, we substitute
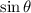 to find
to find
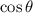 :
:
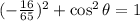 .
.
Solving for
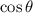 , we have
, we have
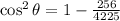 ,
,
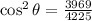 .
.
Taking the square root of both sides gives
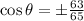 .
.
We found before that since the angle theta terminates in quadrant 4, the cos is positive, so we take the positive square root to get
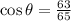 .
.