Question

If a triangle has side lengths 7, 10, and 12, is it a right triangle??

Answer 1

No. Remember, a right angle must have a 90 degree angle. We can find the lengths with the Pythagorean Theorem.

Explanation:

Given the length 7, 10, and 12, we can assume that 12 is the hypotenuse (it is the longest length).

- we can use 7 and 10 interchangeably.

Fill in the equation,
`a^2 + b^2 = c^2`

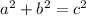
where c = 12, and a or b = 7 or 10.

To indicate if the given lengths would form a right angle, we can only input 7 or 10, not both.

Therefore,
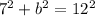`7^2 + b^2 = 12^2` or
`10^2 + b^2 = 12^2`

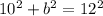
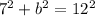`7^2 + b^2 = 12^2` ==> 49 + b^2 = 144 ==> b=
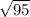`\sqrt{95` ==> 9.746

b= 9.7, not 10.

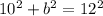`10^2 + b^2 = 12^2` ==> 100 + b^2 = 144 ==> b =
`\sqrt{44` ==> 6.633

b= 6.6, not 7.

Therefore, the lengths 7, 10, and 12, does NOT make a right triangle.

Hope this helps!