Question

Question 12. Is the one I need help on

Answer 1

Four Answers:

• Choice A
• Choice C
• Choice D
• Choice J

====================================================

Step-by-step explanation:

A rational number is any fraction of two whole numbers.

Examples: 7/9 and -8/12

This can be extended to some numbers like
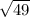`√(49)` because

`√(49) = √(7^2) = 7 = (7)/(1)`

As you can see, any whole number is also rational but not the other way around.

So far, these examples help show that choices A, C, D, and J are rational numbers. Choice D might need a bit of rewriting like so:

`(0.5)/(8) = 0.5 / 8\\\\ = (1)/(2) / (1)/(8) \\\\= (1)/(2) * (8)/(1)\\\\ = (8)/(2)\\\\ = 4`

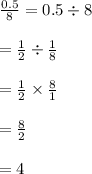
In short, the expression for choice D simplifies to 4 = 4/1 showing that is rational. Or you can use the shortcut that rational/rational = rational.

------------------

A number like
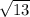`√(13)` is NOT rational because the 13 is not a perfect square. There's no way to rewrite that square root as a ratio or fraction of integers. This allows us to rule out choice B. Choices E, F, and G are eliminated for similar reasoning.

Choice H is ruled out because circle areas involve pi = 3.14159... which is famously an irrational number. The proof of which is very lengthy to go over, but the short version is the decimal digits go on forever without a pattern. This is an informal way to check if we have an irrational number.

Choice I is only eliminated if and only if the side lengths of the square are rational, and also when the side lengths are whole numbers. Its not clear what your teacher's intentions here are, but I'll assume this is the case.

------------------

To summarize, we eliminated B, E, F, G, H, I

We're left with A, C, D, J as the final answers. They either can be written as fractions of integers, or already are fractions of integers.