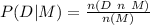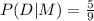Question

The positions on a lacrosse team are called defenders (D). midfielders (M) and attackers (A) One player is chosen at random to lead the team in

exercises before each game. The letters MDD mean that a midfielder was chosen at the first game and a defender was chosen at the next two

games. The list of all possible outcomes is shown, where each outcome has equal probability of occurring.

MDA

DDA

AMA

AMM

AAA

AAM

AAD

ADA

ADM

ADD

DMA

DMM

MAA

MAM

MAD

MMA

MMM

DDM

DAA

DAM

DAD

MDM

MDD

MMD

DMD

AMD

DDD

What is the probability that a defender is chosen at least once, given that a midfielder is chosen at the first game?

Answer 1

`P(D|M) = (5)/(9)`

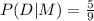
Explanation:

Given

The sample space

Required

Probability that D is chosen at least twice provided that M is chosen first

First, list out all outcomes where M is selected first

`M = \{MDA,,MAA,MAM,MAD,MMA,MMM,MDM,MDD,MMD\}`

`n(M) = 9`

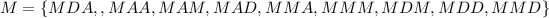
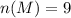
Next, list out all outcomes where D appears at least 1 when M is first

`D\ n\ M= \{MDA,MAD,MDM,MDD,MMD\}`

`n(D\ n\ M) = 5`

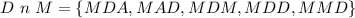
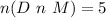
So, the required probability is:

`P(D|M) = (n(D\ n\ M))/(n(M))`

`P(D|M) = (5)/(9)`