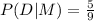Answer:
Explanation:
Given
The sample space
Required
Probability that D is chosen at least twice provided that M is chosen first
First, list out all outcomes where M is selected first
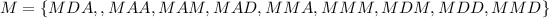
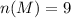
Next, list out all outcomes where D appears at least 1 when M is first
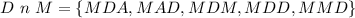
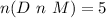
So, the required probability is: